Казино всегда выигрывает

Два математика, Майкл Смолл (Michael Small) и Чи Кон Це (Chi Kong Tse), опубликовали работу, в которой предложили систему выигрыша в рулетку. Эта новость мгновенно разлетелась по Сети и, будучи помноженной на природное нелюбопытство (в саму заметку удосужились заглянуть только единицы) и всеобщую неграмотность в простейших вопросах физики и теории вероятностей, разрослась до совершенно невероятных масштабов. На «Ленте.ру», например, она стала самой читаемой новостной заметкой за 14 мая. Что же конкретно сделали ученые и действительно ли им, открывшим тайну азартной игры, в которой проигрывают миллионы, теперь следует опасаться за свою жизнь? Давайте разберемся.

Из прошлого

Рулетка — пожалуй, одна из самых популярных азартных игр на сегодняшний день — впервые появилась во Франции. По одной из версий (приводимой Эриком Беллом в книге «Men Of Mathematics», опубликованной в 1937 году), руку к изобретению рулетки приложил Блез Паскаль. Согласно этой версии, колесо с дефлекторами должно было стать одной из деталей вечного двигателя, над которым работал ученый. По другим версиям, игру с колесом придумали в Древнем Китае, французском монастыре или в Италии. Последняя версия замечательна тем, что в ней фигурирует некто Дон Паскуале (Don Pasquale), то есть человек с почти такой же, как и у Паскаля, фамилией. Впрочем, «Дон Паскуале» — это еще и опера-буффа конца XIX века, поэтому существование итальянского математика с таким именем вызывает сомнение.

Как бы то ни было, но в конце XVIII века рулетка, известная также как чертово колесо (сумма всех чисел на диске равна в точности 666), завоевала Францию. Отчасти это было связано с тем, что игра выглядела много честнее — то есть случайнее — других, существовавших на тот момент. В самой первой версии рулетки по ободу игрового колеса имелись 36 выемок, в которых были расставлены числа от 1 до 36 — в первой версии рулетки не было сектора зеро. Этот сектор, как ниже станет ясно из математической модели рулетки, нужен для того, чтобы в некотором смысле казино всегда выигрывало. Эту оплошность (отсутствие зеро) к началу XIX века исправили, а спустя некоторое время, когда рулетка добралась до США, на колесе появился 38-й сектор — дабл-зеро, который увеличил среднюю прибыль казино почти в два раза.

Впрочем, и здесь есть альтернативная версия событий: существует мнение, что колесо с одним зеро было придумано позже, чем с двумя. Называют даже конкретные имена изобретателей «более честной рулетки»: Франсуа и Луи Бланк. Якобы они впервые представили рулетку с одним зеро в своем казино в немецком курортном городке Бад-Хомбурге в 1843 году. Эту гипотезу, однако, старательно распространяли сами братья, про одного из которых ходила легенда, что он продал душу дьяволу, поэтому эта версия вызывает серьезные сомнения.

Правила игры

Изображение рулетки XVIII века

Итак, обратимся к основным правилам игры в рулетку, которые, за исключением некоторых несущественных нюансов, не менялись практически с конца уже упомянутого XVIII века. Основным инструментом игры является колесо. Оно представляет собой некоторую наклонную воронкообразную поверхность (обычно не слишком высокую — края воронки не должны закрывать от участников игры движение шарика). На дне поверхности установлено колесо, по краям которого располагается 37 (в американской версии 38) секторов, также ограниченных дефлекторами. В этих секторах проставлены числа от 0 до 36. Зеро покрашено в зеленый, в то время как остальные сектора — в черный или красный цвета (обоих цветов одинаковое количество). Числа на ободе расположены не по порядку, однако, за этим, скорее, стоит традиция, нежели математика. Если считать от зеро по часовой стрелке, то числа идут в следующем порядке: 0, 32, 15, 19, 4, 21, 2, 25, 17, 34, 6, 27, 13, 36, 11, 30, 8, 23, 10, 5, 24, 16, 33, 1, 20, 14, 31, 9, 22,18, 29, 7, 28, 12, 35, 3, 26.

Игрокам, которых может быть несколько, разрешается делать ставки, причем одна ставка может охватывать группу чисел в количестве 1, 2, 3, 4, 12, 18. Крупье раскручивает колесо в одну сторону, а по наклонной поверхности в противоположную пускает маленький шарик. Со временем скорость шарика снижается и он сваливается на колесо, где в конце концов оказывается в одной из лунок. После того как шарик остановился, всем игрокам выплачивается выигрыш, а проигравшие ставки забирает себе казино. Выигрыш рассчитывается по несложной формуле (36 — n)/n к 1, где n — количество чисел в группе, на которую ставил игрок. В правилах некоторых казино случай выпадения зеро описан отдельно: например, игорный дом может не забирать все ставки игроков сразу, а предложить им на выбор либо вернуть половину ставки сейчас, либо дать ей сыграть еще раз.

Какие же бывают ставки? По традиции, никак не связанной с математикой, они делятся на внутренние и внешние. Чтобы сделать ставку, игрок кладет некоторое количество фишек, обозначающих деньги, на фиксированный участок игрового поля. Само поле состоит из множества секторов. Основную его часть занимают числа от 1 до 36, расположенные в трех секторах по 12 в каждом, вместе с четвертым, целиком занятым нулем. Это и есть внутренняя часть поля. По ее краям расставлены специальные сектора, означающие внешние ставки. Примечательно, что европейская рулетка обычно отличается большими по величине полями — из-за их размера крупье для перемещения ставок по столу использует специальную лопаточку, в то время как их американские коллеги предпочитают действовать руками.

На самом деле, как станет понятно из математической модели, рулетка устроена так, что казино безразлично, какие ставки совершает игрок — имеют значения только размеры ставок. Более того, используя приведенную выше формулу, можно разрешить игрокам ставить на любые комбинации, содержащие до 18 чисел (это условие нужно, чтобы выигрыш соотносился со ставкой как целое число — выплачивать, например, 1/35 ставки может быть не очень удобно). Однако, по традиции, которой уже более 200 лет, ставки принимаются только на некоторые фиксированные наборы чисел:

Прямая ставка (Straight Bet). Это просто ставка на номер, включая зеро. В этом случае n = 1 и выигрыш составляет 35 к 1
Ставка на два номера (Split Bet). Ставить можно на два соседних на столе номера (включая зеро) — это, разумеется, не все возможные пары. В этом случае n = 2 и выигрыш составляет 17 к 1
Ставка на три номера (Street Bet). Ставить можно на три номера в одном столбце (зеро, по понятным причинам, не включается). В этом случае n = 3 и выигрыш составляет 11 к 1
Из-за особенностей расположения зеро отдельно выделяют ставку трио (Trio) — это ставка на тройки (0,1, 2) и (0, 2, 3). Тут тоже n = 3 и выигрыш составляет 11 к 1
Угловая ставка (Corner Bet). Ставят на четыре соседних номера на столе. В этом случае n = 4 и выплата составляет 8 к 1
Из-за особого расположения зеро, как и в случае с трио, существует ставка, именуемая корзиной (Basket) — это ставка на (0,1, 2, 3). Выигрыш, как и в предыдущем случае, составляет 8 к 1
Две линии (Line Bet) — ставка на два соседних столбца, по три числа в каждом. Тут n = 6 и выигрыш составляет 5 к 1

Внешние ставки обещают выигрыш гораздо меньший, чем внутренние:

Колонка (Column Bet) — ставят на 12 номеров, расположенных в одной строке таблицы. Выигрыш равен двойной ставке
Дюжина (Dozen) — ставка делается на три возможных числовых промежутка: от 1 до 12, от 13 до 24 или от 25 до 36. Выигрыш тут тоже равен двойной ставке
Змейка (Snake) — ставка делается на 1, 5, 9, 12, 14, 16, 19, 23, 27, 30, 32 и 34. Название становится понятным, если взглянуть на расположение этих чисел на столе. Эта ставка встречается не во всех казино, и выигрыш, как и в предыдущих двух случаях, составляет 2 к 1
Ставки чет-нечет (угадывается четность выпавшего числа), красное-черное (угадывается цвет числа), от 1 до 18, от 19 до 36 (в обоих случаях игрок ставит на то, что выигравшее число попадет в указанные границы) приносят выигрыш равный ставке. Их обычно обозначают термином равные деньги (Even Money)

Теперь, когда правила игры (более или менее) ясны, самое время обратиться к способам, позволяющим эти правила обойти, коих за более чем 200-летнюю историю существования казино накопилось немало. Все эти способы можно разделить на две категории — теоретические и практические (речь, конечно, идет о способах, не связанных с непосредственным воздействием на крупье или саму рулетку). Поговорим вначале о теоретических способах.

Вероятность и математическое ожидание

Стол и колесо для игры в рулетку
(Нажмите, чтобы увеличить)

Сложно сказать, что заставляет людей верить в существование неких таинственных алгоритмов, которые должны обеспечить выигрыш в рулетку. Возможно, не последнюю роль тут играет пресловутая сумма чисел, равная 666, возможно — банальное невежество в области теории вероятностей, помноженное на веру в чудеса (есть же люди, которые верят, что МММ победит законы рынка). Как бы то ни было, но слухи о существовании таких таинственных закономерностей ходили со времени появления игры.

Для того чтобы понять, на чем они основаны, необходимо коротко рассказать о математической модели рулетки. Пространство возможных исходов состоит из 37 элементов, вероятность выпадения каждого из которых равна 1/37. Предположим, что игрок ставит на группу из n чисел. Составляем уравнение для случайной величины — она принимает значение -m в случае, когда число из группы не выпадает, то есть в 37 — n из 37 случаев (m — размер ставки, а знак минус показывает, что деньги мы теряем), и (36 — n)m/n, когда число из группы выпадает.

Эта величина моделирует процесс игры. Для нее мы можем посчитать так называемое математическое ожидание — характеристику, описывающую среднее значение величины. Не вдаваясь в подробности (их можно найти, например, здесь ) скажем, что оно равно — m/37, что составляет примерно -0,027m (кстати, в случае с американской рулеткой с дабл-зеро потери составляют почти в два раза больше). Здесь видно, зачем в игру был добавлен сектор зеро — если бы его не было, математическое ожидание равнялось бы нулю (по сути это происходит из-за того, что в формуле выигрыша фигурирует число 36, а секторов на колесе — 37) и игра шла бы с казино на равных, что, конечно, для последнего совершенно неприемлемо.

Приведенная математика является иллюстрацией прекрасного выражения «Выиграть в рулетку можно, выигрывать — никогда». Построение всякой системы выигрыша в рулетку обычно опирается на простое соображение: в общем случае игрок определяет только один параметр игры — размер ставки. При этом, в силу случайности процесса, он имеет на руках только информацию о своих или чужих проигрышах на данный момент.

Тройка, семерка, туз

Таким образом, всякая стратегия выигрыша в рулетку представляет собой по сути рекуррентную последовательность ставок m_k. где каждая ставка определяется как функция от ставок с номерами меньшими k и задаваемых ими случайных величин. Так уж повелось, что от математики обычно ждут ответа на вопрос «Как выиграть?», в то время, как она говорит, что всякая определенная подобным образом стратегия для достаточно больших промежутков времени приводит к проигрышу.

Вместе с тем, стратегии «с обрывом» существуют. Простейшая из них — это так называемый мартингейл (или мартингал, мартингал Даламбера и прочие). Итак, в рамках этой стратегии предлагается ставить всегда на равные деньги, например, чет-нечет, с каждым ходом увеличивая ставку в два раза. Если первая ставка m, то через k подряд идущих проигрышей размер ставки составит 2 k m. Если эта ставка выиграла, то мы вернули деньги и получили 2 k m прибыли. Если теперь сложить по формуле геометрической прогрессии все проигранные к этому моменту деньги и вычесть их из выигрыша, то выяснится, что наша прибыль составила всего m, то есть равна первоначальной ставке.

У этой стратегии, известной с XVIII века (примечательно, что до сих пор, спустя более чем два века, находятся люди, рассказывающие содержание этой стратегии как откровение), есть два недостатка: во-первых, для небольшого выигрыша нам нужно очень много денег, а, во-вторых, во всех без исключения современных казино для игроков определен максимальный размер ставки. Это делает мартингейл убыточной глупостью. Модификацией мартингейла является так называемая голландская система, в рамках которой ставки увеличиваются по нечетным числам — то есть, если ставка составляла (2k — 1)m, то на следующем шаге она должна составлять (2k + 1)m. Максимальный размер ставки этой системе мешает меньше, однако одного выигрыша, чтобы покрыть все убытки, недостаточно.

Особняком идет целый класс методов, основанных на интуитивном (и, разумеется, математически неверном) представлении о вероятности. К этому классу, например, относится система биарриц. Суть ее состоит в следующем: за 36 вращений рулетки в среднем выпадает 24 номера. Соответственно, как минимум 12 номеров играют больше одного раза. Метод выглядит так: игрок наблюдает за игрой, не делая ставок. Как только появился повторяющийся номер, он немедленно ставит на него одну и ту же сумму 36 раз подряд. Если за это время номер выпадет всего один раз, то игрок вернет деньги, а если больше, то он будет в плюсе!

Тут, однако, подводит вот какой факт — каждое следующее вращение рулетки не зависит от предыдущего, поэтому эта система эквивалентна совсем глупой и прямолинейной — 36 раз подряд ставить на один и тот же номер. Вероятность выпадения фиксированного номера в серии из 36 вращений составляет примерно 0,63 и не зависит от номера.

Несовершенство мира 1: плохое колесо

Самый простой способ победы в рулетку обеспечивает недостаточно сбалансированное колесо. Этот вариант хорошо описан в рассказе Джека Лондона «Малыш видит сны «. Один из главных героев рассказа, Смок, замечает что колесо, расположенное рядом с печкой в казино «Олений рог», ведет себя странно. Оказалось, что оно покоробилось, а владельцы этого не заметили. Благодаря своей наблюдательности Смок не только выигрывает деньги, но и позже продает «систему» игры владельцу заведения.

Кадр из фильма Раймондаса Вабаласа «Смок и Малыш»

Наиболее популярной историей такого рода из претендующих на достоверность является история господина Джаггера (в некоторых источниках он фигурирует как Уилльям Джаггер или Джозеф Джаггер). Этот господин, будучи механиком и математиком-любителем, в 1937 году в одном из казино в Монте-Карло решил использовать несовершенство существовавших тогда механизмов рулетки. Вместе с шестью помощниками он в течение 5 недель собирал статистику по каждому из шести колес в зале казино. Затем, используя эти сведения, он стал выигрывать и в общей сложности унес из заведения 65 тысяч франков.

Аналогичная история, произошедшая, правда, уже в 1948 году в Аргентине, была описана в журнале Time от 1951 года. Хотя и там не обошлось без художественного налета: главными героями истории были нацистский моряк, несколько фермеров, официант и спекулянты.

До математического совершенства этот метод был доведен в 40-х годах прошлого века, когда сразу несколько математиков предложили удобные методы (тесты) для анализа статистики рулетки на предмет наличия некоторых технических дефектов. Нужно ли говорить, что почти сразу эти методы были взяты на вооружение владельцами казино.

Несовершенство мира 2: детерминизм против случайности

Второй, куда более изощренный способ победить рулетку, связан с тем фактом, что, вообще говоря, так как игра происходит макрообъектами, то говорить о случайности нельзя в принципе. То есть описанная выше математическая модель просто неплохо описывает рулетку, в то время как на самом деле знание первоначального положения шарика, его скорости относительно колеса и некоторых других параметров движения в идеале должно дать нам возможность предсказать, куда в конечном счете приземлится шарик.

В начале прошлого века Анри Пуанкаре в работе Science and Methods изучал движение рулетки (правда, без шарика) и установил, что положение, в котором колесо останавливается, очень сильно зависит от первоначальных данных. Отсюда великий математик и физик заключил, что разумной теории предсказания положения рулетки быть не может в принципе. Позже требование зависимости от начальных условий появилось в теории хаоса — в этом смысле работу Пуанкаре с рулеткой можно считать одной из первых по этой столь популярной в нематематических кругах математической теории.

В 1967 году математик Ричард Эпштейн в своей книге The theory of Gambling and statistical logic объявил, что знание первоначальной угловой скорости шарика относительно колеса позволяет предсказать, в какой половине этого самого колеса остановится шарик. Более того, он продемонстрировал, что задача сводится к тому, чтобы определить момент, когда шарик покинет наклонную поверхность вокруг колеса — это происходит при постоянной скорости, поэтому ее также не надо считать. Тогда многие специалисты заключили, что, даже если такие эксперименты проводились, то в реальном времени это сделать было заведомо невозможно — на тот момент просто не существовало подходящих ресурсов.

Лас-Вегас. Фото Reuters

В 1969 году Эдвард Торп опубликовал статью в журнале Review of the International Statistical Institute. в которой сообщил удивительный факт. Оказывается, стремление казино снизить систематическое отклонение от идеальной случайной статистики приводит к тому, что предсказать движения шарика оказывается проще. Дело в том, что при настройке ось колеса иногда наклоняют. Торп показал, что наклона в 0,2 градуса достаточно для того, чтобы на воронкообразной поверхности появился достаточно большой участок, с которого шарик никогда не соскакивает на колесо. Более того, использование для оценки скорости портативного компьютера позволяет довести матожидание выигрыша до 0,44 от ставки! При этом практическая часть исследования, проходившая в Лас-Вегасе, показала, что в среднем треть всех рулеток удовлетворяет условиям, рассмотренным в задаче Торпа.

Следуя работам Торпа, в 1977-1978 годах математики Дуайн Фармер вместе с Норманом Пакардом создали группу, целью которой было выигрывание у казино денег на науку. Группа получила наименование Eudaemons и использовала для работы компьютер на базе процессора 6502, который был спрятан в ботинке одного из участников группы. Разумеется, математической статьи об этой деятельности не появилось, а все произошедшее было описано в книге «Ньютоновское казино» (Newtonian Casino) Томаса Басса, вышедшей в 1990 году.

Наконец, последняя история такого рода произошла в 2004 году, когда трое человек, описанные в новостях как венгерка и двое сербов, выиграли 1,3 миллиона фунтов в казино Ritz в Лондоне. Сделать им это помогли обычный лазерный сканер, мобильный телефон и компьютер. Злоумышленников арестовали, но судья постановил, что, так как они не воздействовали на оборудование казино, деньги были выиграны честно. Имена героев так и не были раскрыты.

Правда или вымысел?

Работа Майкла Смолла (Michael Small) и Чи Кон Це (Chi Kong Tse), препринт которой доступен на сайте arXiv.org, по сути посвящена простому вопросу: есть ли в историях про Eudaemons и отель Ritz доля истины? Насколько вообще возможно предсказывать работу рулетки в реальном времени? Сомнение в реальности описанных событий сохранялись из-за недостаточной математической обоснованности заявлений (например, в работе Торпа многие расчеты были оставлены за кадром).

В рамках работы ученые построили довольно простую динамическую модель движения шарика в рулетке (надо сказать, что существуют более серьезные и реалистичные модели, которые, впрочем, сложнее и с вычислительной точки зрения), а также подходящее программное обеспечение. Авторы проводили опыты двух типов — простой (без дополнительной аппаратуры на столе) и сложный (специальная камера была установлена прямо над колесом). Для опытов использовалось стандартное колесо диаметром 820 миллиметров под названием President Revolution.

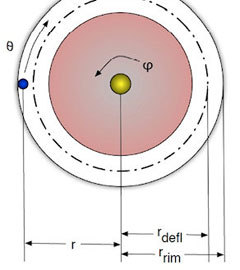
Основные параметры, необходимые для работы анализа Смолла и Це
(Нажмите, чтобы увеличить)

В обоих случаях исследователям необходимо было определить пять параметров. При этом авторы работы, вообще говоря, не заботились о том, чтобы считать эти параметры тайно — все эксперименты проводились в лаборатории и в настоящие казино никто не ездил. При этом исследователи полагались на некоторые технические приспособления, простейшим из которых можно считать мобильный телефон. Как бы то ни было, но в таком простом режиме ученым удалось добиться математического ожидания в 0,18 от ставки (напомним, что сами казино существуют на скромные 0,027 от ставки игрока).

Из этого исследователи делают вывод, что все описанные истории вполне могут оказаться правдой. Примечательно, что Фармер уже прокомментировал работу и заявил, что опубликованный подход очень похож на использованный членами Eudaemons, за исключением правда, некоторых деталей математической модели — Фармер с коллегами считали, что на остановку шарика влияют не те силы, которые работают в работе Смолла и Кон Це.

Как бы то ни было, но защита от новой системы достаточно проста: нужно закрывать ставки до того, как можно будет посчитать скорость вращения шарика и колеса. Оно и понятно, ведь физики и не гнались за баснословными выигрышами — в данном случае их интересовал вопрос правдивости легендарных историй. Таким образом вывод, как и 200 лет назад, для игроков по-прежнему неутешителен: казино всегда выигрывает.